剪绳子

一根长度为n的绳子，请把绳子剪成m段（n > 1且m > 1），每段绳子的长度记为k[0], k[1], ..., k[m]。请问k[0] * k[1] * , ..., * k[m]的可能最大乘积是多少？

class Solution {
    public int maxMulti(int n) {
        if (n < 2) return 0;
        if (n < 4) return n - 1;
        int[] back = new int[n + 1]{0, 1, 2, 3};
        int max = 0;
        for (int i = 4; i <= n; i++) {
            max = 0;
            for (int j = 1; j <= i / 2; j++) {
                int temp = back[j] * back[i - j];
                if (temp > max) max= temp;
            }
            back[i] = max;
        }
        return back[n];
    }
}

• 思路：使用动态规划，记录长度为i时乘积最大值。注意在取[0, 3]时分情况，因为题目要求至少剪一刀，所以在n为[0, 3]时的返回值和记录初始化时的[0, 3]不同。

机器人的运动范围

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

class Point {
    int x;
    int y;
    public Point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}
class Solution {
    private int addSingle(int n) {
        int result = 0;
        while (n > 0) {
            result += n % 10;
            n /= 10;
        }
        return result;
    }
    private boolean check(int x, int y, int k, boolean[][] visited) {
        if (
                x < 0 ||
                y < 0 ||
                x >= visited.length ||
                y >= visited[0].length ||
                visited[x][y]
        ) return false; // [1]
        return addSingle(x) + addSingle(y) <= k;
    }
    public int movingCount(int threshold, int rows, int cols) {
        if (threshold < 0 || rows== 0 || cols == 0) return 0;
        if (threshold == 0) return 1;
        // 初始化访问标记矩阵
        boolean[][] visited = new boolean[rows][cols];
        for (boolean[] lb: visited) {
            lb = new boolean[cols];
            for (boolean b: lb) {
                b = false;
            }
        }
        // BFS
        Queue<Point> queue = new LinkedList<>();
        queue.add(new Point(0, 0));
        Point current;
        int result = 1;
        visited[0][0] = true;
        while (!queue.isEmpty()) {
            current = queue.poll();
            if (check(current.x - 1, current.y, threshold, visited)) {
                queue.add(new Point(current.x - 1, current.y));
                visited[current.x - 1][current.y] = true;
                result++;
            }
            if (check(current.x + 1, current.y, threshold, visited)) {
                queue.add(new Point(current.x + 1, current.y));
                visited[current.x + 1][current.y] = true;
                result++;
            }
            if (check(current.x, current.y - 1, threshold, visited)) {
                queue.add(new Point(current.x, current.y - 1));
                visited[current.x][current.y - 1] = true;
                result++;
            }
            if (check(current.x, current.y + 1, threshold, visited)) {
                queue.add(new Point(current.x, current.y + 1));
                visited[current.x][current.y + 1] = true;
                result++;
            }
        }
        return result;
    }
}

• 思路：没有使用书上的解法，使用BFS，用队列实现。注意[1]处边界条件。

索引和算法

B+树

• B+树是一种平衡查找树。在B+树中，所有记录节点都是按键值的大小顺序存放在同一层的叶子节点上，由各叶子节点指针进行连接。如果用户从最左边的叶子节点开始遍历，可以得到所有键值的顺序排序。

插入操作

• Leaf Page未满，Index Page未满：直接插入即可。

• Leaf Page已满，Index Page未满：需要拆分Leaf Page，将中间节点放入Index Page中，小于中间节点的记录放左边节点，大于或等于中间节点的记录放右边节点。

• Leaf Page已满，Index Page已满：需要拆分Leaf Page和Index Page。拆分Leaf Page同上；拆分Index Page时，小于中间节点的索引放左边，大于中间节点的索引放右边，中间节点放入上一层Index Page。

删除操作

• B+树使用填充因子来控制树的删除变化，50%是填充因子可设置的最小值。
• 叶子节点和中间节点都不小于填充因子：直接删除，如果该节点还是Index Page的节点，用该节点的右节点代替。

• 叶子节点小于填充因子，中间节点不小于填充因子：合并叶子节点和它的兄弟节点，同时更新Index Page。
• 叶子节点和中间节点都小于填充因子：合并叶子节点和它的兄弟节点，更新Index Page，然后合并中间节点和它的父节点、兄弟节点。

B+树索引

• B+树索引的本质是B+树在数据库中的实现。但是B+树索引在数据库中具有高扇出性的特点。因此在数据库中，B+树的高度一般都在2~4层。

扇入：指直接调用该模块的上级模块的个数。扇入大表示模块的复用程序高。

扇出：是指该模块直接调用的下级模块的个数。在此处表示向下查询次数较少。

聚集索引

• 聚集索引就是按照每张表的主键构造一棵B+树，同时叶子节点中存放的即为整张表的行记录数据，也将聚集索引的叶子节点称为数据页。聚集索引的这个特性决定了索引组织表中数据也是索引的一部分。
• 每张表有且只有一个聚集索引。在多数情况下，查询优化器倾向于采用聚集索引，因为聚集索引能够在B+树索引的叶子节点上直接找到数据。此外，由于定义了数据的逻辑顺序，聚集索引能够特别快地访问针对范围值的查询，查询优化器能够快速发现某一段范围的数据页需要扫描。对于主键的排序查找和范围查找速度非常快。
• 聚集索引的存储并不是物理上连续的，而是逻辑上连续的。

辅助索引

• 辅助索引中，叶子节点并不包含行记录的全部数据。叶子节点除了包含键值以外，每个叶子节点中的索引行还包含了一个书签，该书签用来告知InnoDB存储引擎与索引相对应行数据的位置。

Cardinality值

• 当某个字段可取值范围很小（例如性别、地区、类型等），称为低选择性，对该字段添加B+树索引是完全没有必要的。相反，如果某个字段的取值范围很广，几乎没有重复，即属于高选择性，则此时选择B+树索引是最合适的。
• Cardinality值非常关键，表示索引中不重复记录数量的预估值。在实际应用中，Cardinality / n_rows_in_table应尽可能地接近1。

B+树索引的使用

联合索引

• 联合索引是指对表上的多个列进行索引。以(a, b)为例，首先对于单列a来说，联合索引也是可以使用的，但是单独对b的查询不能使用。如果是需要对多个键进行排序，由于联合索引已经对后面的键进行了排序处理，此时使用联合索引可以减少一次排序操作。

覆盖索引

• 覆盖索引是指从辅助索引中就可以得到查询记录，而不需要查询聚集索引中的记录。辅助索引不包含整行记录的所有信息，因此其大小要远小于聚集索引，因此可以减少大量的IO操作。例如针对一些统计问题，例如count，如果表中有辅助索引，那么没有必要去查询聚集索引。

哈希算法

自适应哈希索引

• InnoDB存储引擎使用哈希算法来对字典进行查找，其冲突机制采用链表方式，哈希函数采用出发散列方式。
• 自适应哈希索引采用上述方式实现。自适应哈希索引经哈希函数银蛇到一个哈希表中，因此对于字典类型的查找非常快速。

全文检索

倒排索引

• 全文检索通常使用倒排索引来实现。它在辅助表中存储了单词与单词自身在一个或多个文档中所在的位置之间的映射。有两种表现形式：
  • inverted file index，{单词，单词所在的文档ID}
  • full inverted index，{单词，(单词所在文档ID，在文档中的具体位置)}

InnoDB全文检索

• InnoDB存储引擎采用full inverted index 的方式实现全文检索。为了提高检索性能，共有6张辅助表，有一个全文检索索引缓存。全文检索索引缓存是一个红黑树结构，在插入数据已经更新到了对应的表时，辅助表的数据可能还没有更新，其更新数据还在全文索引缓存中。当对全文检索进行查询时，首先会将在全文索引缓存中的数据合并到辅助表中，然后在进行查询。

限制

• 每张表只能有一个全文索引。
• 由多页组合而成的全文索引列必须使用相同的字符集与排序规则。
• 不支持没有单词界定符的语言，例如中文、日语等。

表（二）

视图

• 在MySQL数据库中，视图是一个命名的虚表，它由一个SQL查询来定义，可以当作表使用。与持久表不同的是，视图中的入局没有实际的物理存储。

视图的作用

• 视图的主要用途之一是被用作一个抽象装置，特别是对于一些应用程序，程序本身不需要关心基表的结构，只需要按照视图的定义来取数据或更新数据，因此，视图同时在一定程度上起到一个安全层的作用。

• 用户可以对某些视图进行更新操作，一般称可以进行更新操作的视图为可更新视图。如果加上with check option选项，MySQL数据库会对更新视图插入的数据进行检查，对于不满足视图定义条件的插入会抛出一个异常，不允许视图中数据更新。

分区表

• 分区的过程是将一个表或索引分解为多个更小、更可管理的部分。就访问数据库而言，从逻辑上讲，只有一个表或一个索引，但是在物理上这个表或索引可能由数十个物理分区组成。每个分区都是独立的对象，可以独自处理，也可以作为一个更大的对象的一部分进行处理。
• 水平分区是指将同一表中不同行的记录分配到不同的物理文件中，垂直分区是指将同一表中不同列的记录分配到不同的物理文件中。MySQL数据库支持的分区类型为水平分区，不支持垂直分区。
• 局部分区索引是指一个分区中既存放了数据又存放了索引。与之相对的是全局分区，数据存放在各个分区中，但是所有数据的索引放在一个对象中。MySQL的分区是局部分区索引。
• 分区主要用于数据库高可用性的管理。
• 不论创建何种类型的分区，如果表中存在主键或唯一索引时，分区列必须是唯一索引的一个组成部分。如果建表时没有指定主键，唯一索引，可以指定任何一个列为分区列。

分区类型

range分区

• 基于属于一个给定连续区间的列值对行数据进行分区。

create table t (
id int
)engine=innodb
partition by range(id) (
partition p0 values less than (10),
partition p1 values less than (20)
);

list分区

• 同range分区，只是list分区面向的是离散值。如果插入的值不在分区定义中，MySQL数据库会抛出异常。

create table t (
a int,
b int
)engine=innodb
partition by list(b) (
partition p0 values in (1, 3, 5, 7, 9),
partition p1 values in (0, 2, 4, 6, 8)
);

hash分区

• 根据用户自定义的表达式的返回值来进行分区，返回值不能为负数。此外还需要指定分区数量。

create table t (
a int,
b datetime
)engine=innodb
partition by hash (year(b))
partitions 4;

key分区

• 使用MySQL数据库提供的函数进行分区。

create table t (
a int,
b datetime
)engine=innodb
partition by key(b)
partitions 4;

columns分区

• 可以直接使用非整型的数据进行分区，分区根据类型直接比较而得。支持的类型有所有整数类型（int、smallint、tinyint、bigint），日期类型（date、datetime），字符串类型（char、varchar、binary、varbinary）。

create table t (
a int,
b datetime
)engine=innodb
partition by range columns(b) (
partition p0 values less than('2009-01-01'),
partition p1 values less than('2010-01-01')
);

子分区

• 子分区是在分区的基础上再进行分区，有时也称这种分区为复合分区。MySQL数据库允许在range和list分区上再进行hash或key分区。

create table ts (
    a int, 
    b date
)engine=innodb
partition by range(year(b))
subpartition by hash(to_days(b))
subpartitions 2 (
    partition p0 values less than (1990),
    partition p1 values less than (2000),
    partition p2 values less than maxvalue
);

分区中的null值

• MySQL数据库总是认为null值小于任何一个非null值。
• 对于range分区，如果向分区列插入了null值，则MySQL数据库会将该值放入最左边的分区。
• 在list分区中使用null值，必须显式指定在哪个分区放入null值，否则会报错。
• hash和key分区的任何分区函数都会将含有null值的记录都返回0。

尝试使用GitHub Actions自动部署Hexo

参考链接。

• 生成ssh部署公私钥

ssh-keygen

• 为Page仓库添加公钥：
  • Github：在仓库/Settings/Deploy keys中添加，授予写权限
  • Coding：在仓库/设置/部署公钥中添加，授予写权限
• 为源码仓库添加私钥：
  • Github：在仓库/Settings/Secrets中添加，注意记录名称。这个功能可以放一些隐私内容，包括私钥、token、密码等等。
• 编写workflow，文件位置.github/workflows/deploy.yml

name: Node CI

on: [push]

jobs:
  build:

    runs-on: ubuntu-latest

    strategy:
      matrix:
        node-version: [10.x]

    steps:
    - uses: actions/checkout@v1
    - name: Use Node.js 10.x
      uses: actions/setup-node@v1
      with:
        node-version: '10.x'
    - name: env prepare
      env:
        ACTIONS_PRI: ${{secrets.ACTIONS_PRI}}
      run: |
        mkdir -p ~/.ssh/
        echo "$ACTIONS_PRI" > ~/.ssh/id_rsa
        chmod 600 ~/.ssh/id_rsa
        ssh-keyscan github.com >> ~/.ssh/known_hosts
        ssh-keyscan git.coding.net >> ~/.ssh/known_hosts
        git config --global user.name 'SinLapis'
        git config --global user.email 'stradust0001@gmail.com'
        npm i -g hexo-cli
        npm install hexo-renderer-jade hexo-renderer-stylus --save
        npm i
    - name: gen
      run: |
        hexo g -d

多部署注意把域名加入~/.ssh/known_hosts，否则会部署失败。

表（一）

索引组织表

• 在InnoDB存储引擎中，表都是根据主键顺序组织存放的，这种存储方式的表称为索引组织表。如果在创建表时没有显式地指定主键，则InnoDB会按以下方式选择或创建主键：
  • 首先判断表中是否有非空的唯一索引，如果有则该列为主键。该方式选择的根据是定义索引的顺序，而不是建表时列的顺序。
  • 否则，InnoDB存储引擎会自动创建一个6字节大小的指针。

InnoDB逻辑存储结构

• 从InnoDB存储引擎的逻辑存储结构看，所有数据都被逻辑地存放在一个空间中，称之为表空间。表空间又由段、区、页组成。
• 表空间可以看作是InnoDB存储引擎逻辑结构的最高层 ，所有数据都存放在表空间中。
• 常见的段有数据段、索引段、回滚段等。数据段即为B+树的叶子节点，索引段为B+树的非叶子节点。
• 区是由连续页组成的空间，在任何情况下每个区的大小都为1MB。为了保证区中页的连续性，InnoDB存储引擎一次从磁盘中申请4~5个区。在默认情况下，InnoDB存储引擎页大小为16KB，即一个区中一共有64个连续的页。
• 页是InnoDB磁盘管理的最小单位。

约束

数据完整性

• 关系性数据库和文件系统的一个不同点是，关系数据库本身能保证存储数据的完整性，不需要应用程序的控制，而文件系统一般需要在程序端进行控制。
• 一般来说，数据完整性有以下三种形式：
  • 实体完整性保证表中有一个主键，可以通过定义Primary Key或Unique Key约束或者定义一个触发器来保证实体的完整性。
  • 域完整性保证数据每列的值满足特定的条件，可以选择合适的数据类型确保一个入局值满足特定条件，使用外键约束，编写触发器，或者考虑DEFAULT约束。
  • 参照完整性保证两张表之间的关系。可以使用外键以强制参照完整性，也可以使用触发器。
• InnoDB存储引擎提供了以下几种约束：primary key、unique key、foreign key、default、not null

约束的创建

• 约束的创建有两种方式：
  • 表建立时就进行约束定义
  • 利用alter table命令来进行创建约束
• 对于主键约束而言，其默认约束名为primary。对于unique key约束而言，默认约束名和列名一样，也可以人为指定名字。

约束和索引的区别

• 当用户创建了一个唯一索引就创建了一个唯一的约束。约束偏向于一个逻辑概念，用来保证数据完整性，而索引是一个数据结构，既有逻辑上的概念，在数据库中还代表着物理存储方式。

对错误数据的约束

• 在某些魔神设置下，MySQL数据库允许非法的或者不正确的数据插入或更新，又或者可以在数据库内部将其转化为一个合法的值。

触发器约束

• 触发器的作用是在执行insert、delete、update命令之前或之后自动调用SQL命令或存储过程。最多可以为一个表建立6个触发器，即分别为insert、update、delete的before和after各定义一个。当前MySQL数据库只支持for each row的 触发方式，即按每行记录进行触发。
• 通过触发器，用户可以实现MySQL数据库本身并不支持的一些特性。

create table user_cash (
    user_id int not null ,
    cash int unsigned not null 
);

insert into `user_cash`(`user_id`, `cash`) value(1, 1000);
# 非正常行为
update `user_cash` set `cash` = `cash` - (-20) where `user_id` = 1;

# 添加触发器和错误日志
create table `user_cash_err_log` (
    user_id int not null ,
    old_cash int unsigned not null ,
    new_cash int unsigned not null ,
    user varchar(30),
    time datetime
);

create trigger tgr_user_cash_update before update on `user_cash`
    for each row
    begin
        if new.`cash` - old.`cash` > 0 then
            insert into `user_cash_err_log`
            select old.`user_id`, old.`cash`, new.`cash`, USER(), NOW();
            set new.`cash` = old.`cash`;
        end if;
    end;

# 再次尝试非正常行为
update `user_cash` set `cash` = `cash` - (-20) where `user_id` = 1;
select * from user_cash_err_log;
# 1    1020    1040    root@localhost    2019-08-29 10:06:27
select * from user_cash;
# 1    1020

外键约束

• 一般称被引用表为父表，引用的表称为子表。外键定义时的on delete和on update表示在对父表进行delete和update操作时，对子表所做的操作。
• 可定义的子表操包括cascade、set null、no action、restrict。cascade（级联）表示当父级发生delete或update操作时，对相应的子表中的数据也进行delete或update操作。set null表示父表发生delete或update操作时，相应的子表中的数据被更新为null值，但是子表中相对应的列必须允许为null值。no action和restrict在MySQL中等价，都表示父表发生delete或update操作时抛出错误，不允许这类操作发生。

矩阵中的路径

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如 a b c e s f c s a d e e 矩阵中包含一条字符串”bccced”的路径，但是矩阵中不包含”abcb”路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

class Point {
    int x;
    int y;
    public boolean[] visited = {false, false, false, false};

    public Point(int x, int y) {
        this.x = x;
        this.y = y;
    }

    @Override
    public boolean equals(Object obj) {
        try {
            return x == ((Point) obj).x && y == ((Point) obj).y;
        } catch (ClassCastException ce) {
            return super.equals(obj);
        }
    }

}

public class Solution {
    private void resetMB(boolean[][] mb) {
        for (boolean[] bs : mb) {
            for (boolean b : bs) {
                b = false;
            }
        }
    }

    public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
        int firstRow = 0, firstCol = 0;
        char[][] mc = new char[rows][cols];
        boolean[][] mb = new boolean[rows][cols];
        resetMB(mb);
        for (int i = 0; i < rows; i++) {
            mc[i] = new char[cols];
            for (int j = 0; j < cols; j++) {
                mc[i][j] = matrix[i * cols + j];
            }
        }
        while (true) {
            // 先定位第一个字符
            outer:
            for (; firstRow < rows; firstCol = 0, firstRow++) { //[1]
                for (; firstCol < cols; firstCol++) {
                    if (matrix[firstRow * cols + firstCol] == str[0]) break outer;
                }
            }
            if (firstRow >= rows) return false;
            Stack<Point> route = new Stack<>();
            route.push(new Point(firstRow, firstCol));
            int strIndex = 1;
            if (strIndex >= str.length) return true; //[2]
            resetMB(mb);
            mb[firstRow][firstCol] = true;
            // 在定位周围找下一个字符
            while (!route.isEmpty()) {
                Point current = route.peek();
                int visitOri = -1;
                if (
                        current.x - 1 >= 0 &&
                                !current.visited[0] &&
                                !mb[current.x - 1][current.y] &&
                                mc[current.x - 1][current.y] == str[strIndex]
                ) {
                    //0
                    route.push(new Point(current.x - 1, current.y));
                    route.peek().visited[1] = true;
                    visitOri = 0;
                    mb[current.x - 1][current.y] = true;
                    strIndex++;
                } else if (
                        current.x + 1 < rows &&
                                !current.visited[1] &&
                                !mb[current.x + 1][current.y] &&
                                mc[current.x + 1][current.y] == str[strIndex]
                ) {
                    //1
                    route.push(new Point(current.x + 1, current.y));
                    route.peek().visited[0] = true;
                    visitOri = 1;
                    mb[current.x + 1][current.y] = true;
                    strIndex++;
                } else if (
                        current.y - 1 >= 0 &&
                                !current.visited[2] &&
                                !mb[current.x][current.y - 1] &&
                                mc[current.x][current.y - 1] == str[strIndex]
                ) {
                    //2
                    route.push(new Point(current.x, current.y - 1));
                    route.peek().visited[3] = true;
                    visitOri = 2;
                    mb[current.x][current.y - 1] = true;
                    strIndex++;
                } else if (
                        current.y + 1 < cols &&
                                !current.visited[3] &&
                                !mb[current.x][current.y + 1] &&
                                mc[current.x][current.y + 1] == str[strIndex]
                ) {
                    //3
                    route.push(new Point(current.x, current.y + 1));
                    route.peek().visited[2] = true;
                    visitOri = 3;
                    mb[current.x][current.y + 1] = true;
                    strIndex++;
                } else {
                    Point p = route.pop();
                    mb[p.x][p.y] = false;
                    strIndex--;
                }
                if (strIndex >= str.length) return true;
                if (visitOri >= 0) current.visited[visitOri] = true;
            }
            if (firstCol >= cols - 1) { //[1]
                firstCol = 0;
                firstRow++;
            } else {
                firstCol++;
            }
        }
    }
}

• 思路：先找开始位置，然后在周围找下一个。要保存两种状态，一是当前已经选择的位置（由boolean二维数组保存），二是回溯失败的状态（由Point对象保存）。注意：如果要找下一个初始位置，[1]处要对初始坐标进行处理，包括移动到下一个坐标和一行循环完成置列号为0（因为要保存之前的状态，所以不能在循环列时置0）；[2]处防止不需要进入循环时要返回true的情况。

观察者模式

• 观察者模式定义对象之间的一对多依赖，这样一来，当一个对象改变状态时，它的所有依赖者都会收到通知并自动更新。

松耦合

• 当两个对象之间松耦合，它们依然可以交互，但是互相不关心对方的实现。换句话说，它们各自可以独立复用，在保证交互接口不变的条件下可以修改各自的实现。
• 观察者模式实现了主题和观察者之间松耦合的对象设计。

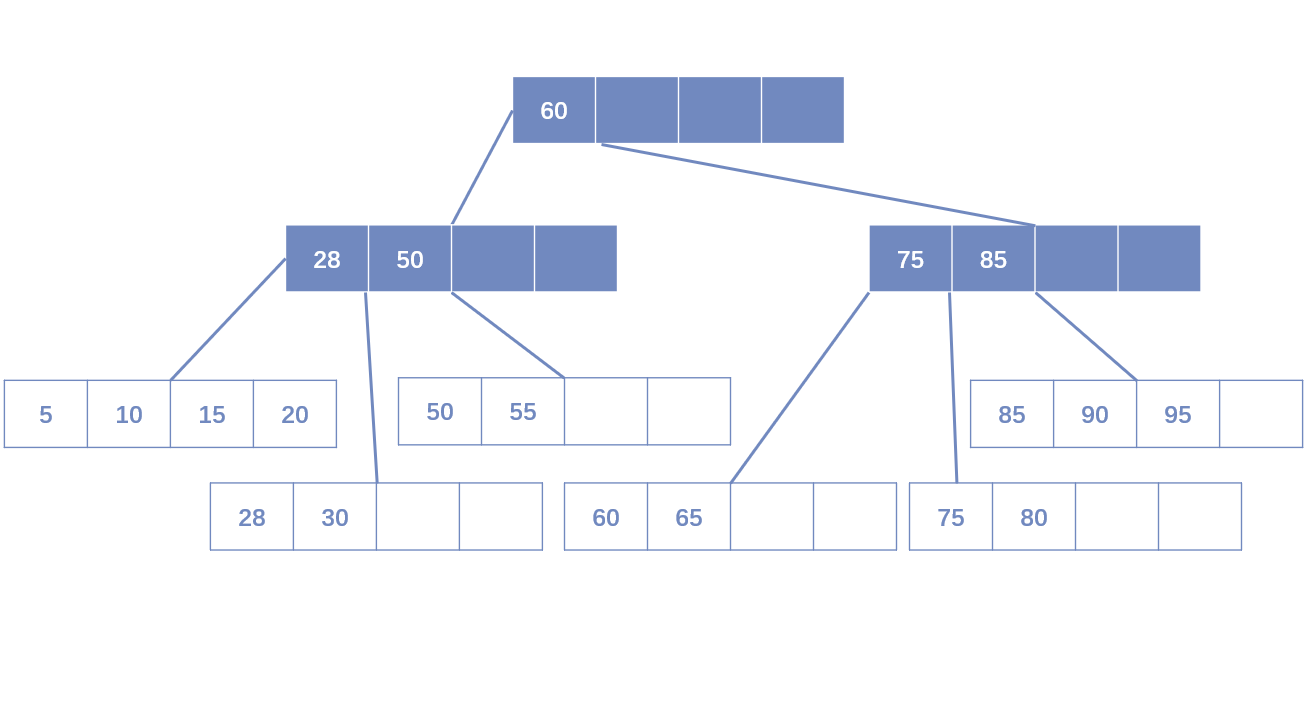
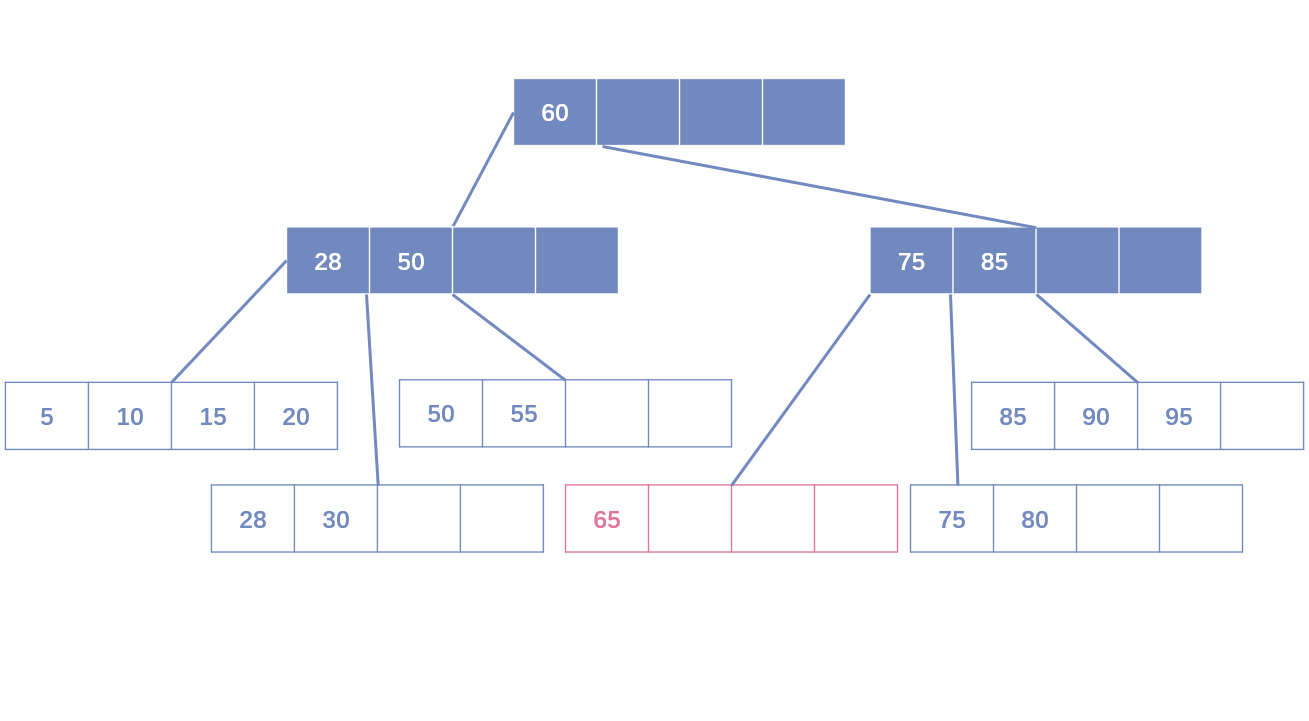
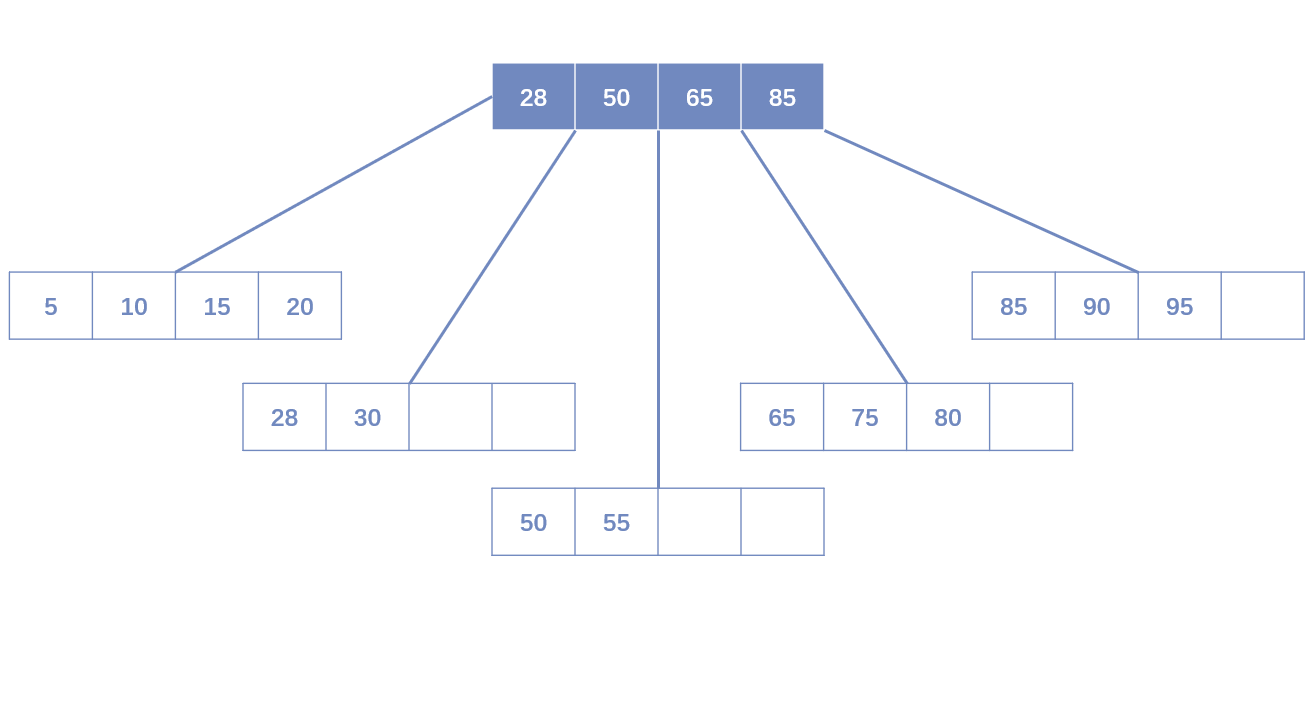
面向对象和函数式编程的混合：Java 8和Scala的比较

Java 与 Scala的混合编程

参考。使用Maven生成项目，pom.xml文件如下：

<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
    <modelVersion>4.0.0</modelVersion>

    <groupId>org.bigmt</groupId>
    <artifactId>mjns</artifactId>
    <version>1.0-SNAPSHOT</version>
    <properties>
        <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
        <java.version>11</java.version>
        <maven.compiler.source>11</maven.compiler.source>
        <maven.compiler.target>${maven.compiler.source}</maven.compiler.target>
    </properties>

    <dependencies>
        <dependency>
            <groupId>org.scala-lang</groupId>
            <artifactId>scala-library</artifactId>
            <version>2.13.0</version>
        </dependency>
        <dependency>
            <groupId>org.scala-lang</groupId>
            <artifactId>scala-compiler</artifactId>
            <version>2.13.0</version>
        </dependency>
        <dependency>
            <groupId>org.scala-lang</groupId>
            <artifactId>scala-reflect</artifactId>
            <version>2.13.0</version>
        </dependency>
    </dependencies>
    <build>
        <plugins>
            <plugin>
                <groupId>org.apache.maven.plugins</groupId>
                <artifactId>maven-compiler-plugin</artifactId>
                <version>3.8.0</version>
                <configuration>
                    <release>11</release>
                </configuration>
            </plugin>
            <plugin>
                <groupId>org.scala-tools</groupId>
                <artifactId>maven-scala-plugin</artifactId>
                <version>2.15.2</version>
                <executions>
                    <execution>
                        <goals>
                            <goal>compile</goal>
                            <goal>testCompile</goal>
                        </goals>
                    </execution>
                </executions>
            </plugin>
        </plugins>
    </build>
</project>

// Main.java
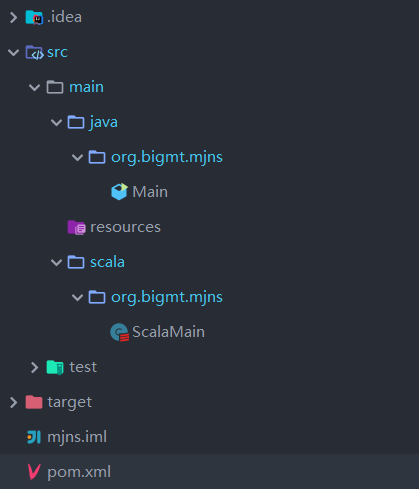
package org.bigmt.mjns;

public class Main {
    public static void main(String[] args) {
        ScalaMain scalaMain = new ScalaMain();
        scalaMain.entry();
    }
}

// ScalaMain.scala
package org.bigmt.mjns

class ScalaMain {
  def entry(): Unit = {
    var n: Int = 2
    while (n <= 6) {
      println(s"Hello ${n} bottles of beer")
      n += 1
    }
  }
}

Scala简介

你好，啤酒

// Scala
2 to 6 foreach {n => println(s"Hello ${n} bottles of beer")}

// Java
IntStream.rangeClosed(2, 6)
    .forEach(n -> System.out.println("Hello " + n + " bottles of beer"));

基础数据结构

创建集合

// Scala
val authorsToAge = Map("Raoul" -> 23, "Mario" -> 40, "Alan" ->53)
val authors = List("Raoul", "Mario", "Alan")
val numbers = Set(1, 1, 2, 3, 5, 8)

不可变

• Scala中不可变的集合是持久化的，更新一个Scala集合会生成一个新的集合，这个新的集合和之前版本的集合共享大部分内容，最终的结果是数据尽可能地实现了持久化。

// Scala
val numbers = Set(2, 5, 3)
val newNumbers = numbers + 8
println(numbers)
println(newNumbers)
/* Output:
Set(2, 5, 3)
Set(2, 5, 3, 8)
*/

使用集合

// Scala
val fileLine = List("test", "test for scala", "no vac", "yeeeeeeees man")
val linesLongUpper = fileLine.par.filter(_.length() > 10).map(_.toUpperCase())
println(linesLongUpper)
/* Output
List(TEST FOR SCALA, YEEEEEEEES MAN)
*/

旋转数组的最小数字

快速排序

public class Q11_0 {
    public void quickSort(int[] arr, int start, int end) {
        if (start > end) return;
        int i = start, j = end;
        int t = arr[i];
        while (i < j) {
            while (i < j && t <= arr[j]) j--;
            if (i < j) {
                arr[i] = arr[j];
                i++;
            }
            while (i < j && t > arr[i]) i++;
            if (i < j) {
                arr[j] = arr[i];
                j--;
            }
        }
        arr[i] = t;
        quickSort(arr, start, i - 1);
        quickSort(arr, j + 1, end);
    }
}

旋转数组的最小数字

public class Q11 {
    public int minNumberInRotateArray(int[] array) {
        if (array == null || array.length == 0) return 0;
        int left = 0, right = array.length - 1;
        int mid;
        while (left < right) {
            mid = left + right >> 1;
            if (array[left] < array[right]) return array[left];
            if (array[mid] > array[left]) left = mid + 1;
            else if (array[mid] < array[left]) right = mid;
            else left++;
        }
        return array[right];
    }
}

• 思路：和书上略有不同，主要是处理相同数字上。如果arr[left]和arr[mid]相等，那么只移动left即可。此外，要比较arr[left]和arr[right]的大小，否则会越过最小值。